La Inteligencia Artificial al servicio de la desintegración radiactiva

La inteligencia artificial (IA) ha revolucionado numerosos campos, desde la medicina hasta las finanzas. Sin embargo, una de las áreas más sorprendentes donde la IA está dejando su huella es en el estudio de la radiactividad.

A primera vista, puede parecer una combinación extraña, pero la capacidad de la IA para analizar grandes cantidades de datos y detectar patrones complejos la convierte en una herramienta invaluable para comprender fenómenos tan intrincados como la desintegración radiactiva.

La ley de desintegración radiactiva describe cómo los núcleos inestables se transforman en núcleos más estables a lo largo del tiempo, un proceso que puede ser modelado matemáticamente.

Tipos de desintegraciones radiactivas

La desintegración radiactiva es un fenómeno natural por el cual un núcleo atómico inestable pierde energía al emitir radiación. Existen varios tipos de desintegraciones radiactivas, entre las cuales destacan:

1. Desintegración alfa (α): En este tipo de desintegración, un núcleo emite una partícula alfa (dos protones y dos neutrones). Esto resulta en una disminución del número atómico en 2 y del número másico en 4. Es común en elementos pesados como el uranio y el radio.
2. Desintegración beta (β): Esta desintegración implica la conversión de un neutrón en un protón (o viceversa) dentro del núcleo, acompañada por la emisión de una partícula beta (un electrón o un positrón). La desintegración beta puede ser clasificada como beta negativa (β-) o beta positiva (β+), dependiendo del tipo de partícula emitida. En el primer caso un neutrón se convierte en un protón, emitiendo un electrón y un antineutrino. Por otro lado, hablaremos de desintegración β+ cuando un protón se convierta en un neutrón, emitiendo un positrón y un neutrino.
3. Desintegración gamma (γ): A menudo ocurre después de una desintegración alfa o beta, donde el núcleo emite radiación gamma para liberar energía adicional sin cambiar su número atómico o másico. No se trata de una desintegración en sí, sino la emisión de radiación electromagnética de alta energía cuando un núcleo pasa de un estado excitado a uno de menor energía.
4. Captura electrónica: En este proceso, un protón del núcleo captura un electrón orbital, convirtiéndose en un neutrón y emitiendo un neutrino. Esto también resulta en una disminución del número atómico.
5. Fisión espontánea: En ella, algunos núcleos pesados se dividen espontáneamente en fragmentos más ligeros, liberando neutrones y energía

Cada uno de estos tipos de desintegraciones tiene implicaciones diferentes tanto para la física nuclear como para aplicaciones prácticas en medicina, energía nuclear y otros campos.

Ley exponencial de desintegración

La ley de desintegración radiactiva se describe mediante una función exponencial que relaciona el número de núcleos radiactivos presentes con el tiempo transcurrido. Matemáticamente, se expresa como:

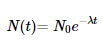
Donde:

• N(t) es el número de núcleos restantes en el tiempo (t).
• N0 es el número inicial de núcleos.
• λ es la constante de desintegración específica para cada isótopo.
• e es la base del logaritmo natural.

Esta ecuación muestra que el número de núcleos radiactivos disminuye exponencialmente con el tiempo. La constante λ está relacionada con la vida media T1/2 del isótopo a través de la relación:

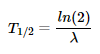
Esto significa que después de cada intervalo igual a una vida media, aproximadamente la mitad del material original habrá decaído.

Esta ley exponencial tiene aplicaciones interesantes en IA, particularmente en el diseño de redes neuronales y en la optimización de algoritmos de aprendizaje. Por ejemplo, las funciones de activación en redes neuronales a menudo utilizan formas exponenciales similares a la ley de desintegración radiactiva.

Ecuaciones de Bateman

Las ecuaciones de Bateman, desarrolladas por Harry Bateman, describen la evolución temporal de una cadena de desintegraciones radiactivas.  Estas ecuaciones son fundamentales para describir procesos complejos donde hay múltiples etapas o productos intermedios en las reacciones nucleares y permiten calcular las cantidades relativas de diferentes isótopos a lo largo del tiempo cuando hay varias etapas involucradas en la descomposición.

Para un sistema con n isótopos que se descomponen secuencialmente, las ecuaciones pueden expresarse como:

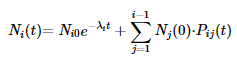
Donde:

• Ni(t) es el número del isótopo (i) en el tiempo (t).
• Pij(t) representa las probabilidades asociadas a las transiciones entre los isótopos.

Estas ecuaciones son especialmente útiles en estudios sobre residuos nucleares y procesos industriales donde múltiples isotopos están presentes simultáneamente. En el contexto de la IA, las ecuaciones de Bateman pueden inspirar modelos para sistemas complejos con múltiples estados interconectados, como en el procesamiento del lenguaje natural o en la modelización de sistemas ecológicos.

Propiedades estadísticas y fluctuaciones estadísticas

La naturaleza aleatoria del proceso de desintegración radiactiva introduce propiedades estadísticas significativas. Aunque se puede predecir cuántos núcleos permanecerán después de cierto tiempo utilizando la ley exponencial, no se puede predecir exactamente cuándo ocurrirá cada evento individualmente. Esto da lugar a fluctuaciones estadísticas que pueden ser modeladas usando distribuciones probabilísticas.

Distribución binomial

En contextos donde se estudian grandes cantidades de núcleos radiactivos, se puede utilizar la distribución binomial para modelar el comportamiento estadístico del proceso. Si consideramos un gran número N0 de núcleos inicialmente presentes y asumimos que cada núcleo tiene una probabilidad p = 1 – e-λt de haber decaído después del tiempo t, entonces podemos aplicar la distribución binomial:

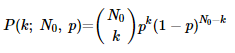
Donde:

• P(k; N0, p) es la probabilidad de que exactamente k núcleos hayan decaído.

• (N0:k) es el coeficiente binomial que cuenta las combinaciones posibles.

   

Este enfoque permite realizar predicciones sobre cuántas partículas han decaído tras cierto periodo y proporciona información valiosa sobre los riesgos asociados con materiales radiactivos. La naturaleza estadística de la desintegración radiactiva ofrece paralelismos interesantes con los procesos estocásticos en IA. Esta distribución tiene aplicaciones en IA, particularmente en problemas de clasificación binaria y en el diseño de funciones de pérdida para modelos de aprendizaje automático.

Un nuevo horizonte

La exploración de las conexiones entre la IA y la ley de desintegración radiactiva revela sorprendentes paralelismos y oportunidades de aprendizaje mutuo. Los principios estadísticos y matemáticos que gobiernan la desintegración radiactiva ofrecen inspiración para el desarrollo de algoritmos de IA más robustos y eficientes.

Por otro lado, las técnicas de IA pueden mejorar nuestra capacidad para modelar y predecir procesos radiactivos complejos. Al integrar técnicas avanzadas basadas en IA —como aprendizaje automático— podríamos optimizar modelos predictivos relacionados con procesos nucleares y mejorar nuestra capacidad para gestionar residuos radiactivos o desarrollar nuevas tecnologías energéticas más seguras.

La combinación del conocimiento físico con herramientas computacionales avanzadas promete abrir nuevas fronteras tanto en investigación científica como en aplicaciones prácticas relacionadas con la energía nuclear y su impacto ambiental.