Hexadecimal
El sistema hexadecimal, también conocido como base 16 o simplemente hex, es un sistema de numeración que utiliza 16 símbolos diferentes para representar los valores numéricos. En el sistema hexadecimal, los valores van desde 0 a 9 para representar los primeros 10 dígitos, y las letras A, B, C, D, E y F (o a, b, c, d, e, f) se utilizan para representar los valores del 10 al 15, respectivamente.
El sistema hexadecimal se utiliza ampliamente en informática y programación debido a su estrecha relación con el sistema binario. Cada dígito hexadecimal representa exactamente 4 bits binarios (medio byte), lo que facilita la conversión y manipulación de datos en formato binario.
Sistema hexadecimal, decimal y binario
Hay tres sistemas numéricos comúnmente utilizados en informática: decimal, binario y hexadecimal. El sistema decimal es el que utilizamos en nuestra vida cotidiana, con 10 dígitos (0-9). El sistema binario, utilizado internamente por los ordenadores, utiliza solo dos dígitos (0 y 1). El sistema hexadecimal actúa como un puente entre los sistemas decimal y binario, ya que es fácil de convertir entre binario y hexadecimal y viceversa.
Tabla de conversión hexadecimal, decimal y binario
A continuación, se muestra una tabla de conversión entre los sistemas hexadecimal, decimal y binario para los 16 primeros valores:
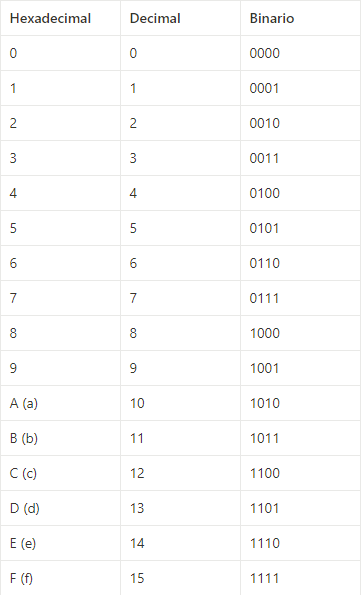
Para convertir números hexadecimales a binarios, se pueden sustituir directamente cada dígito hexadecimal por su equivalente binario de 4 bits.
Cómo contar en hexadecimal
Cuando contamos en hexadecimal, seguimos un patrón similar al que utilizamos en el sistema decimal. Empezamos con 0 y contando hacia arriba, una vez que llegamos al dígito '9' pasamos a la letra 'A' que representa el valor 10 en decimal, luego continuamos con 'B' (11), 'C' (12), 'D' (13), 'E' (14) y 'F' (15). Una vez que llegamos a 'F', pasamos a '10' (que representa el 16 en decimal), y así continuamos con el patrón.
Ejemplo de conversión de números hexadecimales a binarios y decimales
Para convertir un número hexadecimal a binario, debemos sustituir cada dígito hexadecimal por su equivalente binario de 4 bits. Por ejemplo, el número hexadecimal '2A' se convierte al binario '00101010'.
Para convertir un número hexadecimal a decimal, multiplicamos cada dígito hexadecimal por su posición en base 16 y sumamos los resultados. Por ejemplo, el número hexadecimal '2A' se convierte al decimal de la siguiente manera: 2 * 16^1 + A * 16^0 = 42.
Uso de hexadecimal en colores RGB
El sistema hexadecimal se utiliza también para representar colores RGB y RGBA. En este caso, utilizamos dos dígitos hexadecimales para representar la intensidad de cada uno de los canales de color: rojo (R), verde (G) y azul (B). Por ejemplo, el color magenta se representa como '#FF00FF', donde 'FF' indica la intensidad máxima del rojo y el azul y '00' indica la ausencia de verde.
Uso de hexadecimal en la programación
El uso del sistema hexadecimal en programación resulta práctico, ya que la mayoría de los ordenadores utilizan el sistema binario para almacenar y procesar datos, y la conversión entre hexadecimal y binario es directa y simple. Las representaciones hexadecimales se utilizan en los lenguajes de programación para especificar números, caracteres, colores y direcciones de memoria.
En resumen, el sistema hexadecimal es una herramienta versátil que facilita la representación y manipulación de datos en formato binario, particularmente en el contexto de informática y programación. Su uso en el mundo digital ha demostrado ser una elección eficiente y sencilla para trabajar con grandes cantidades de información en forma compacta y comprensible.