
Matriz de transición y su aplicación en IA y Machine Learning
La matriz de transición es una herramienta matemática fundamental en el estudio de procesos estocásticos, teoría de Markov y modelos de aprendizaje automático. Representa las probabilidades de transición entre distintos estados de un sistema dinámico, siendo particularmente relevante en el modelado del comportamiento secuencial de datos.
Su aplicabilidad en inteligencia artificial abarca modelos de Markov ocultos, redes neuronales recurrentes (RNN) o sistemas de predicción y planificación en entornos inciertos. En este artículo explicaré cómo funciona, su relación con los modelos de Markov y su papel en los sistemas modernos de inteligencia artificial.
Fundamentos de la matriz de transición y aplicaciones en Machine Learning
Una matriz de transición de estados describe las probabilidades de moverse de un estado a otro dentro de un sistema dinámico. En un contexto discreto y finito, si un sistema tiene n estados, la matriz de transición es una matriz cuadrada de tamaño n×n donde cada entrada Pij representa la probabilidad de transición del estado i al estado j.
En machine learning, especialmente en modelos secuenciales, estas matrices permiten representar dinámicas temporales entre observaciones. Algunas de sus aplicaciones más directas son el análisis de comportamiento de usuarios, el modelado de lenguaje natural, la predicción de series temporales y el análisis de cadenas de eventos en sistemas complejos.
Su relación con los modelos de Markov
Los modelos de Markov son estructuras estadísticas que dependen exclusivamente del estado actual del sistema para predecir el siguiente, lo cual se conoce como propiedad de Markov. La matriz de transición de Markov es el componente más importante en estos modelos, permitiendo describir completamente su comportamiento estocástico.
Por ejemplo, en los Modelos de Markov ocultos (HMM), muy utilizados en tareas de reconocimiento de voz, procesamiento de lenguaje natural y bioinformática, las matrices de transición permiten modelar la probabilidad de pasar de un estado oculto a otro. Esto se combina con matrices de emisión para predecir observaciones visibles a partir de estados latentes.
Cómo implementar una matriz de transición en modelos de predicción
La implementación de una matriz de transición en modelos de predicción implica varios pasos:
Definición de estados: determinar el conjunto finito de estados que representan el sistema. Esto puede derivarse directamente de los datos (por ejemplo, categorías discretas) o a través de técnicas de discretización.
Estimación de probabilidades de transición: a partir de una secuencia de observaciones, se cuenta cuántas veces ocurre cada transición y se normaliza para obtener una matriz estocástica. Si Cij es el conteo de transiciones de i a j, entonces Pij=Cij/∑kCik.
Evaluación y ajuste: validar la matriz en datos de prueba y ajustar mediante regularización si existen problemas de sobreajuste o escasez de datos.
En lenguajes como Python se usan librerías como numpy, pandas y hmmlearn para trabajar con matrices de transición de forma eficiente.
Matriz de transición en procesos estocásticos
Desde la perspectiva teórica, una matriz de transición se utiliza en procesos estocásticos para modelar el comportamiento probabilístico de sistemas que evolucionan en el tiempo. Estos procesos son fundamentales para entender fenómenos como las cadenas de suministro, la evolución de los mercados financieros o incluso patrones en secuencias genéticas.
Entre las propiedades clave de estas matrices se encuentran:
Irreducibilidad: todo estado es alcanzable desde cualquier otro.
Periodicidad: patrones cíclicos en las transiciones.
Estacionariedad: existencia de una distribución estable de probabilidad.
En IA, estos conceptos permiten definir el comportamiento a largo plazo de un sistema, lo cual se vuelve imprescindible para tareas como la detección de anomalías o la predicción de comportamiento en el tiempo.
Uso en sistemas de inteligencia artificial
El análisis de una matriz de transición implica examinar sus propiedades algebraicas y estadísticas. Por ejemplo, la distribución estacionaria se obtiene resolviendo πP=π, donde π es un vector fila que representa la distribución de probabilidad estable del sistema.
Esta información es útil para detectar estados recurrentes, evaluar la probabilidad de absorción o calcular medidas de centralidad y persistencia en redes dinámicas.
En sistemas de inteligencia artificial, este análisis permite:
Optimizar la toma de decisiones en entornos probabilísticos.
Evaluar la estabilidad de sistemas autónomos.
Diseñar agentes adaptativos en entornos estocásticos.
Además, las matrices de transición se utilizan como entrada en arquitecturas más complejas como modelos de decisión de Markov (MDP) y procesos de decisión parcialmente observables (POMDP).
Su uso en Redes Neuronales Recurrentes (RNN)
Aunque las redes neuronales recurrentes (RNN) no utilizan matrices de transición explícitas, su comportamiento interno puede modelarse mediante estructuras similares. Las RNN mantienen un estado oculto que se actualiza a lo largo del tiempo en función de la entrada y del estado anterior, de forma análoga a una transición de estado.
En investigaciones recientes, se ha explorado la idea de aproximar o interpretar el comportamiento de RNNs y transformers utilizando marcos estocásticos basados en matrices de transición, con el fin de aumentar la interpretabilidad y estabilidad del aprendizaje.
Además, en tareas de predicción de secuencias o modelado de lenguaje, el análisis de los pesos de una RNN puede revelar patrones similares a los observados en modelos de transición, lo que sugiere una fuerte relación conceptual entre ambas estructuras.
Ejemplo de uso de una matriz de transición con Python
A continuación, se muestra un ejemplo de cómo construir e interpretar una matriz de transición a partir de una secuencia de estados observados usando el lenguajef Python.
Supongamos el siguiente código que simula una secuencia de estados:

La salida esperada sería:
| A | B | C |
A | 0.0 | 0.5 | 0.5 |
B | 1.0 | 0.0 | 0.0 |
C | 0.0 | 0.5 | 0.5 |
Dando un mapa de calor como el siguiente:
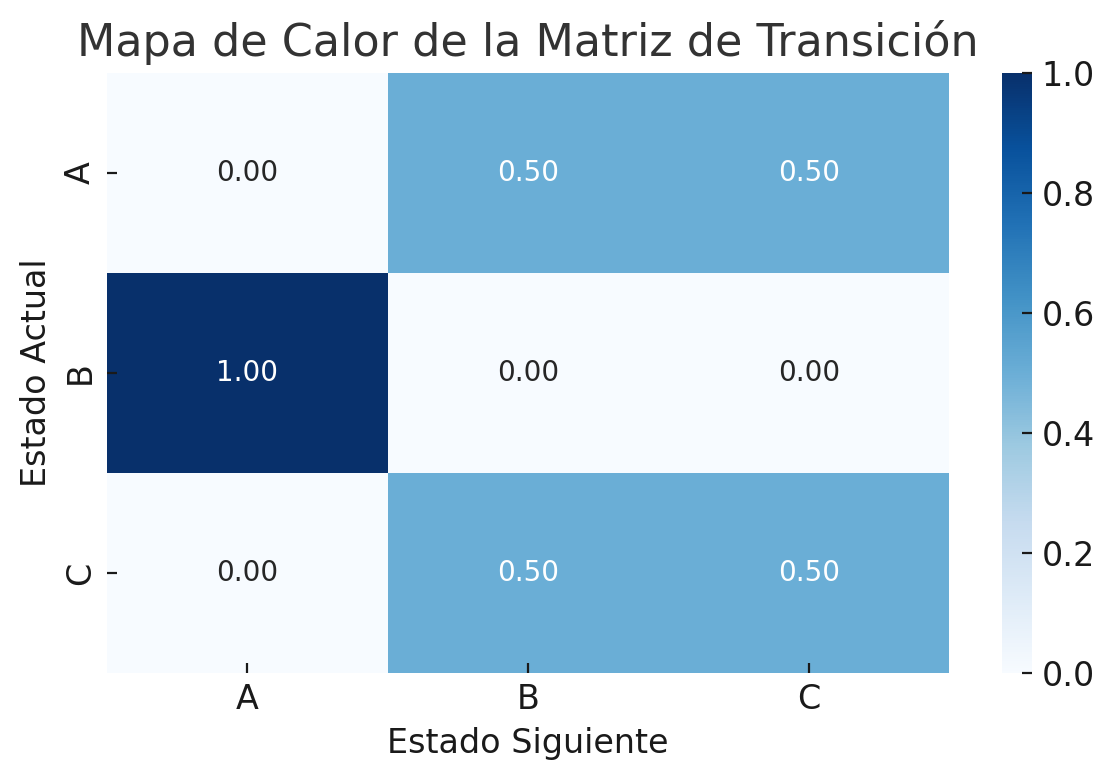
Y en el que la interpretación sería que desde el estado A, hay un 50% de probabilidad de transicionar a B y un 50% a C mientras que, desde B, siempre se transita a A.
Esta matriz se puede utilizar en un modelo de predicción secuencial, como un generador de estados futuros basado en probabilidad.
Tabla comparativa: Tipos de modelos que usan matrices de transición
La siguiente es una tabla comparativa de qué modelos o algoritmos usan matrices de transición, para qué tarea y de qué forma:
Modelo / Algoritmo | ¿Usa Matriz de Transición? | Aplicación Principal | ¿Explícita o Implícita? |
Cadena de Markov | Sí | Modelado de procesos estocásticos | Explícita |
Modelo de Markov Oculto (HMM) | Sí | Reconocimiento de patrones y series temporales | Explícita |
Red Neuronal Recurrente (RNN) | No (pero se puede interpretar) | Modelado secuencial y procesamiento de texto | Implícita |
Proceso de Decisión de Markov (MDP) | Sí | Planificación y control en IA | Explícita |
Transformers (con atención) | No | Modelado de dependencias a largo plazo en secuencias | Implícita (con atención) |
Sistemas de Recomendación Basados en Secuencias | Sí (en versiones simplificadas) | Predicción de próximos ítems en comportamiento de usuario | Explícita o implícita |
Matriz de transición: Base matemática para muchos modelos
Por tanto, se puede afirmar que la matriz de transición es un componente fundamental para muchos de los modelos que hoy día se utilizan en inteligencia artificial y aprendizaje automático.
En el contexto actual, donde anticiparse y adaptarse a los cambios es una necesidad, dominar el uso e interpretación de matrices de transición permite desarrollar modelos más precisos, robustos y explicables.
Si quieres aprender más acerca de cómo sacar el máximo rendimiento a la inteligencia artificial te recomiendo el Máster en Inteligencia Artificial y Data Science.
Artículos relacionados

Robótica cognitiva: una gran oportunidad para la inteligencia artificial
La robótica cognitiva busca comprender los modelos cognitivos que rigen la inteligencia humana y plasmarlos en robots. Su objetivo es hacer posible

Tecnologías futuristas que están a la vuelta de la esquina
En el habla cotidiana, entendemos que lo futurista es una visión orientada al futuro en lo referente a todo el conjunto de dispositivos tecnológicos p

El futuro de la IA: posibles avances y retos
En EducaOpen sabemos de primera mano que el avance de las tecnologías es imparable.
