Evaluación de homogeneidad de varianzas mediante la prueba de Levene

La prueba de Levene es una técnica estadística usada para evaluar la igualdad de varianzas entre dos o más grupos.

En el ámbito de la ciencia de datos e inteligencia artificial, esta prueba es determinante para los análisis donde se aplican técnicas como el test t-student para comparar medias de diferentes grupos o cuando se emplean modelos que asumen varianzas iguales.

A lo largo de este artículo, exploraremos los pasos para realizar una prueba de Levene, sus supuestos, ejemplos aplicados y su interpretación, especialmente cuando se trabaja con datos en software como SPSS o lenguajes de programación como Python o R.

¿Qué es la prueba de Levene y cuándo usarla?

La prueba de Levene (o "test de Levene") es un procedimiento estadístico que verifica si dos o más grupos tienen varianzas iguales.

Este test es una alternativa robusta a la prueba de Baretlett cuando los datos no siguen una distribución normal, siendo particularmente útil cuando los datos presentan distribuciones asimétricas o incluyen valores atípicos.

En el contexto de la ciencia de datos y la inteligencia artificial, la prueba de Levene es un paso preliminar antes de aplicar otras pruebas estadísticas, como la prueba t para muestras independientes.

Las técnicas de machine learning, como ANOVA, regresión lineal o análisis de componentes principales (PCA), requieren frecuentemente el cumplimiento de la homogeneidad de varianzas para garantizar la validez de los resultados.

Supuestos para la prueba de Levene

Antes de llevar a cabo una prueba de Levene, es importante cumplir ciertos supuestos estadísticos:

1. Escala de medida: las variables deben estar en una escala de intervalo o razón.
2. Independencia de observaciones: los grupos deben ser independientes unos de otros.
3. Muestra aleatoria: los datos deben provenir de una muestra representativa y aleatoria.

Aunque el test de Levene no requiere normalidad en los datos, es indispensable asegurarse de que las observaciones dentro de cada grupo sean independientes. En el análisis de datos experimentales o en machine learning, este supuesto suele cumplirse si los datos se han recogido adecuadamente.

¿Cómo hacer una prueba de Levene?

La prueba de Levene se basa en transformar los datos en función de la mediana o media de cada grupo y luego calcular las diferencias absolutas respecto a esos valores centrales.

Estos pasos se pueden ejecutar en plataformas estadísticas como SPSS, Python (con scipy.stats.levene), o R (con leveneTest en el paquete car).

Prueba de Levene en Python

Veamos un ejemplo sencillo del uso de esta prueba utilizando Python. Para ello, hay que seguir los siguientes pasos:

Importar librerías:

Preparar los datos: organizando los datos en grupos separados. Por ejemplo:

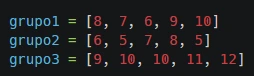
Aplicar la prueba:

Interpretar el resultado: Si el p-valor es menor a un nivel de significancia predeterminado (como 0.05), se rechaza la hipótesis nula de igualdad de varianzas.

Funcionamiento en SPSS

En el caso de SPSS, se deberían de seguir los siguientes pasos para realizar la prueba de Levene:

1. Importar los datos en SPSS y organizar las variables por grupos.
2. Ir a Analyze > Compare Means > One-Way ANOVA.
3. En el menú de opciones, seleccionar Test de Homogeneidad de Varianzas (Prueba de Levene).
4. Interpretar el resultado de acuerdo con el p-valor.

Ejemplo de prueba de Levene en Ciencia de Datos

Supongamos que un científico de datos está trabajando en un modelo de predicción de precios inmobiliarios en varias ciudades. Al comparar los precios en distintas zonas, es necesario asegurar que las varianzas sean homogéneas antes de aplicar un test t-student para evaluar si las medias difieren significativamente.

Veamos cómo podríamos hacerlo paso a paso en Python. Para ello, habría que seguir el siguiente orden:

Definir los grupos:

Realizar la prueba de Levene:

Interpretación: Si el p-valor es menor que 0.05, se rechaza la hipótesis nula, indicando que al menos una de las zonas tiene una varianza significativamente diferente.

Interpretación de la prueba de Levene

Uno de los aspectos más importantes a la hora de sacar conclusiones de la realización de la prueba de Levene es su interpretación.

La prueba de Levene genera dos valores clave: el estadístico de Levene y el p-valor. La interpretación se basa en el p-valor:

• p < 0.05: existe suficiente evidencia para rechazar la hipótesis nula, lo que indica que las varianzas de los grupos no son iguales.
• p ≥ 0.05: no hay suficiente evidencia para rechazar la hipótesis nula, por lo que podemos asumir que las varianzas son homogéneas.

Si el resultado de la prueba de Levene indica desigualdad de varianzas, debe optarse por versiones robustas de los tests que siguen.

Por ejemplo, en lugar de un test t-student estándar para comparar dos medias, sería recomendable aplicar el test de Welch, que ajusta para varianzas desiguales.

En modelos de machine learning, si se observan diferencias significativas en las varianzas, podría ser indicativo de que las clases representan poblaciones diferentes y requeriría una revisión del muestreo o un tratamiento distinto para los datos.

Importancia en Ciencia de Datos e Inteligencia Artificial

La prueba de Levene es fundamental para garantizar que los análisis posteriores sean válidos en contextos como la predicción, clasificación y segmentación de datos.

La homogeneidad de varianzas es un supuesto muy relevante en algoritmos como:

• Regresión lineal múltiple: las varianzas homogéneas aseguran que los errores de predicción se distribuyan de manera uniforme, evitando sesgos en los coeficientes estimados.
• ANOVA y MANOVA: estos análisis son sensibles a la homogeneidad de varianzas. El uso de la prueba de Levene asegura que los resultados obtenidos en comparación de medias entre múltiples grupos sean estadísticamente sólidos.
• Clasificación y clustering: la igualdad de varianzas en diferentes grupos asegura que la segmentación sea homogénea, lo cual facilita la interpretación y robustez de los resultados.

Homogeneidad de varianzas, la clave para validar multitud de análisis

La prueba de Levene es una de esas herramientas que todo científico de datos debe conocer y utilizar para poder validar uno de los supuestos estadísticos fundamentales y, en conjunto con otros análisis como el test t para muestras independientes, refuerza la precisión y confiabilidad de los modelos y análisis.

Para implementar la prueba de Levene, plataformas como SPSS o lenguajes de programación como Python ofrecen métodos rápidos y eficientes, permitiendo evaluar la homogeneidad de varianzas y decidir los siguientes pasos en el análisis estadístico o de machine learning.

Si quieres aprender más sobre esta prueba y otras aplicaciones de la estadística en la programación y la ciencia de datos, te recomiendo nuestro Máster en Formación Permanente en Matemática Computacional.